
Геометрия, 10 класс
Готов
Вопрос от 1807 дней назад
Треугольник АВС правильный, точка О – его центр. Прямая ОМ перпендикулярна к плоскости АВС. а) Докажите, что МА = МВ = МС. б) Найдите МА, если АВ = 6 см, МО = 2 см.
Ответ от
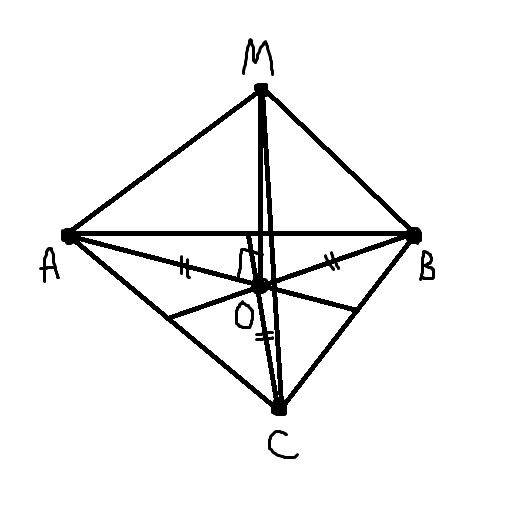
а) В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Центр равностороннего треугольника является центром вписанной и описанной окружностей. АО=ВО=СО - радиусы опис.окружности. МО⟂(АВС), значит ОМ⟂ОА, ОМ⟂ОВ, ОМ⟂ОС. ОМ - общая сторона. Треугольники МОА=МОВ=МОС (по двум катетам), слеловательно их гипотенузы тоже равны, т.е. МА=МВ=МС.
Прочитайте, пожалуйста, правила - в одном вопросе не более одного задания. Каждая буква - отдельное упражнение (т.е. 1 вопрос=1 пример).