
Геометрия, 8 класс
Готов
Вопрос от 1896 дней назад
Решите задания 1. Точки М и Р – середины противоположных сторон ВС и АК параллелограмма АВСК. Докажите, что АМСР – параллелограмм. 2. В трапеции АВСD ВС – меньшее основание. На отрезке АD взята точка Е так, что ВЕ││СD, ÐАВЕ = 70°, ÐВЕА = 50°. Найдите углы трапеции. 3. В прямоугольной трапеции МКРО ÐКМО = 90°, ÐКМР = 45°, ÐКРО = 135°, КР = 7 дм. Найдите меньшую боковую сторону. 4. В ромбе АКСЕ угол К острый, АМ и АР высоты. Угол между диагональю АС и высотой АР равен 25°. Найдите углы ромба. 5. В прямоугольнике АВСD диагонали пересекаются в точке М. Отрезок МК является медианой треугольника АМD, ÐАМК = 72°. Найдите ÐВDС 6. В параллелограмме КМNР проведена биссектриса угла МКР, которая пересекает сторону МN в точке Е. Докажите, что треугольник КМЕ равнобедренный. Найдите сторону КР, если МЕ = 10 см, а периметр параллелограмма равен 52 см. 7. В трапеции АВСD диагональ ВD перпендикулярна боковой стороне АВ, ÐАDВ = ÐВDС = 30°. Найдите длину АD и среднюю линию трапеции, если периметр трапеции 60 см
Ответ от
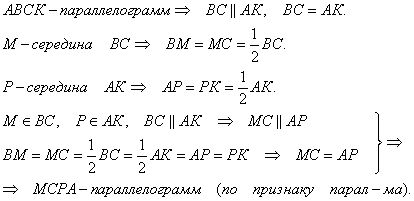
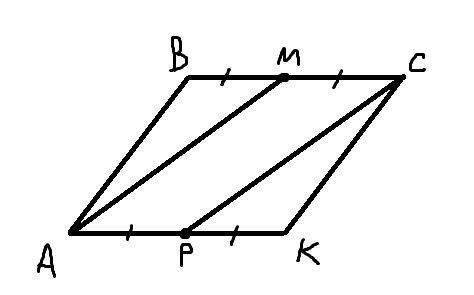
НОМЕР 1.
Прочитайте, пожалуйста, правила - в одном вопросе не более одного задания. Каждая буква - отдельное упражнение (т.е. 1 вопрос=1 пример).