
Математика, 9 класс
Готов
Вопрос от 2627 дней назад
Два луча, образующие угол величиной 46 градусов, высекают из окружности две дуги, большая из которых равна 132градуса.Найдите меньшую дугу и две другие дуги окружности, учитывая, что они относятся как 1:3.
Ответ от
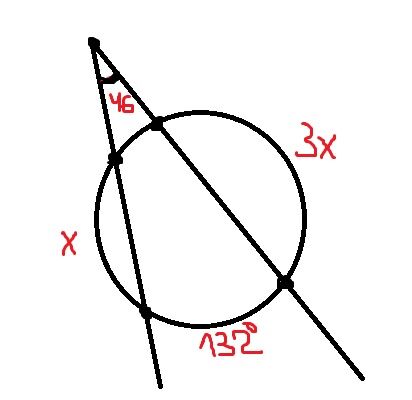
Теорема (угол между секущими): Угол между двумя секущими, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг. Пусть меньшая дуга = с. Получаем: 46° = (132°-с):2 132° - с = 46°*2 132° - с = 92° с = 132° - 92° с = 40° - меньшая дуга. Сумма всех дуг = 360° (окружность). Учитывая, что две другие дуги окружности относятся как 1:3, то одна из них = х, другая = 3х. Получаем уравнение: 132° + 40° + х + 3х = 360° 172° + 4х = 360° 4х = 360° - 172° 4х = 188° х = 188° : 4 х = 47° - первая боковая дуга. 3х = 47°*3 = 141° - вторая боковая дуга. Ответ: 40°, 47°, 141°.
Спасибо!