
Геометрия, 9 класс
Готов
Вопрос от 2639 дней назад
4 задачу,пожалуйста
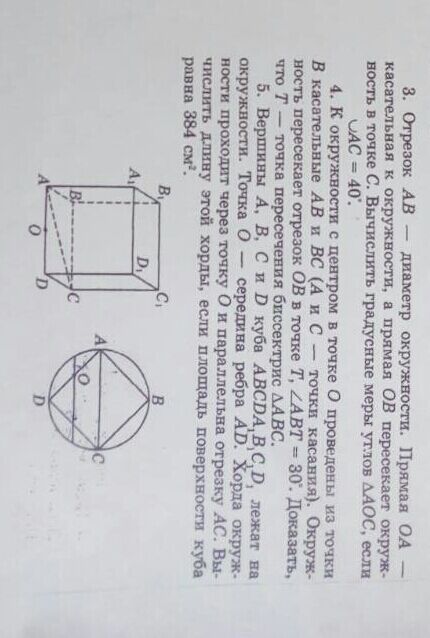
Ответ от
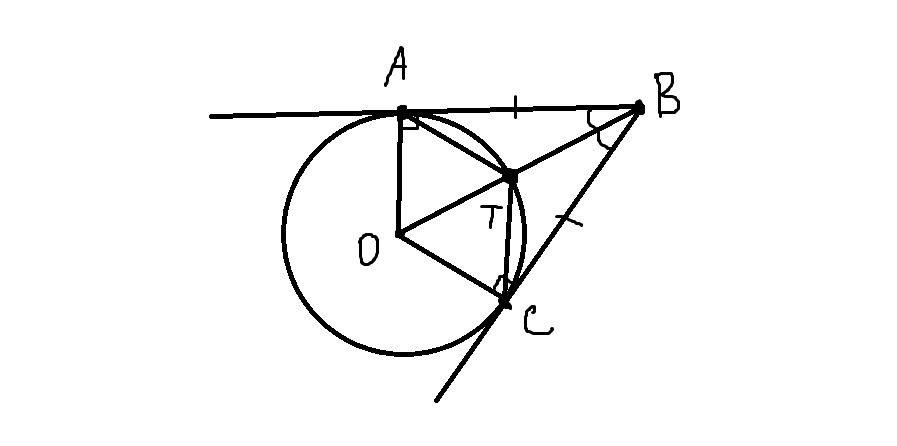

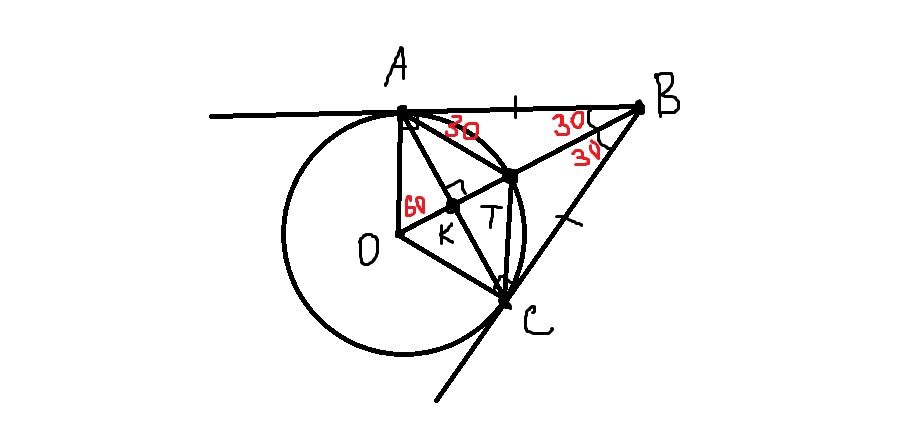
Теорема. Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными. Т.е. АВ=ВС и ВО-биссектриса угла АВС. ВО-биссектриса угла АВС, значит угол АВО=угол СВО=30 градусов. ВА и ВС - касательные к окружности, значит угол ОАВ и угол ВСО - прямые (90 градусов). Следовательно, треугольники ОАВ и ВСО - прямоугольные и равные друг другу (т.к. гипотенуза ВО-общая, а катеты АВ=ВС). Докажем, что АТ - биссектриса угла САВ. (см.рис.2 и 3). Аналогично доказывается, что СТ - биссектриса угла ВСА. ВО, АТ, СТ - биссектрисы, пересекающиеся в точке Т.