Геометрия, 8 класс

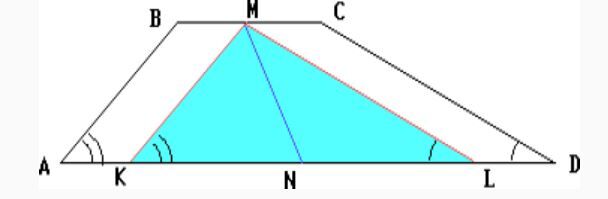
Пусть M и N – середины оснований BC и AD трапеции ABCD (AD > BC) и ∠A + ∠D = 90°. Через точку M проведём прямые, параллельные AB и CD. Пусть K и L – точки их пересечения с основанием AD. ∠A = ∠MKL и ∠D = ∠MLK (как соответствующие углы с секущей AD). Тогда ∠MKL + ∠MLK = ∠A + ∠D = 90°. Поэтому ∠KML = 90° (т.к. сумма углов треугольника равна 180°). NK = AN – AK = AN – BM = DN – CM = DN – DL = NL. Значит, MN – медиана прямоугольного треугольника KML, проведённая из вершины прямого угла. Поэтому 2MN = KL = AD – AK – LD = AD – BM – MC = =AD – BC.