Алгебра, 9 класс

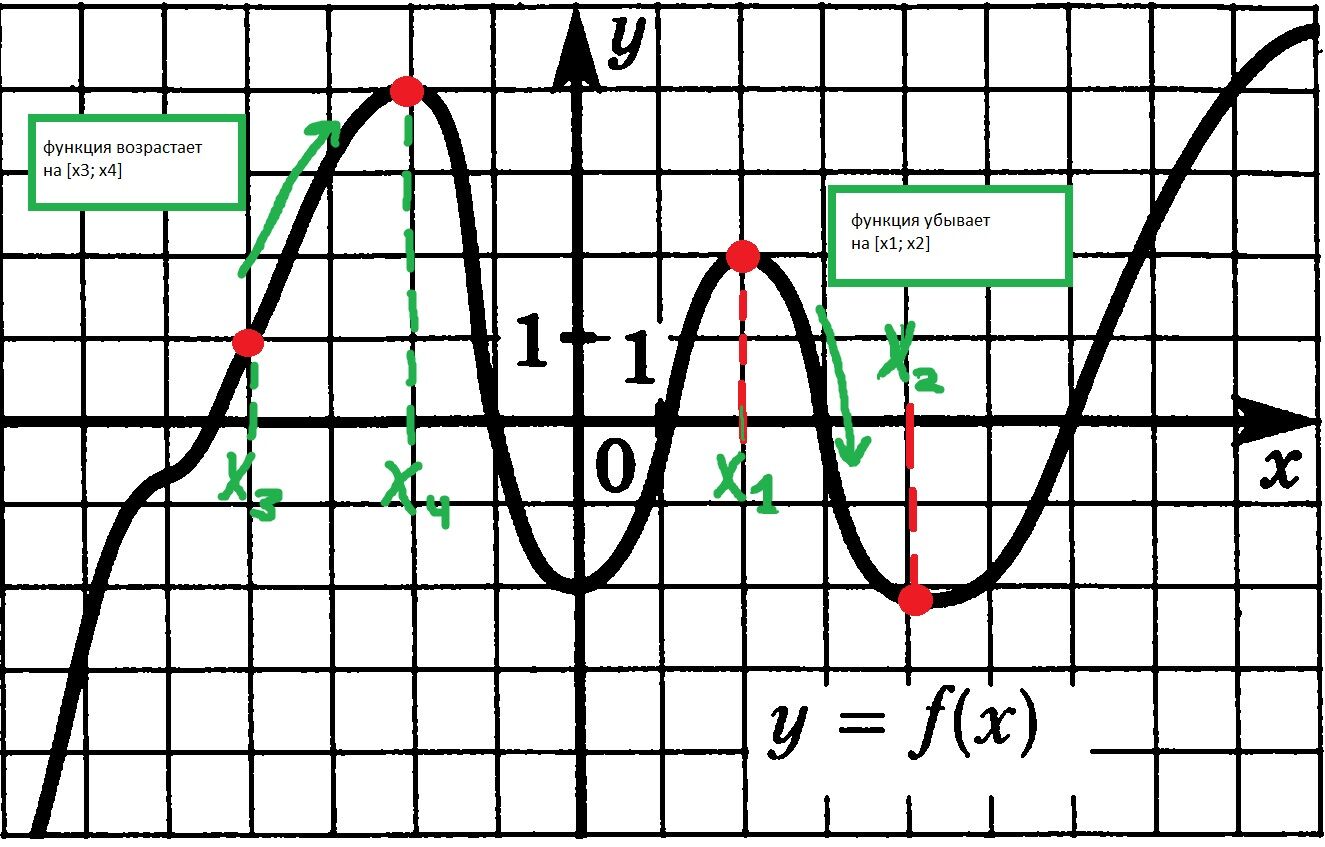
Пусть х1 и х2 - любые действительные числа (из множества R), удовлетворяющие единственному условию х1 < х2. Тогда функция y = f(x) называется: - убывающей на R, если при этом: f(x1) > f(x2); - возрастающей на R, если при этом: f(x1) < f(x2). Иначе говоря, нужно взять разность f(x1) - f(x2) и посмотреть знак этой разности. Если он отрицателен, то функция возрастает на R; если положителен - то убывает на R; а если ноль, то не убывает и не возрастает (к примеру, монотонная). Но это должно выполняться для любых х1 и х2 из области R (области действительных чисел), таких, что x2 > x1. Как только для какой-то пары таких чисел нарушается условие убывания функции, нельзя сказать, что функция убывает на R. С возрастанием - то же самое. Функция может при этом убывать / возрастать на каком-то другом промежутке, отличном от R, но на самом R убывать/возрастать не будет. ПРОЩЕ ГОВОРЯ: Если есть график, то берешь две точки на нем х1 и х2. х1